PID制御とは何か、pythonでシミュレーションをしながら解説します。シミュレーションについては以下の記事で紹介しています。
リンク
まず、質量のある物体( 制御対象 )に力(制御入力)を加え、ある値に収束させることを考えます。
下図は縦軸が位置、横軸が時間を表しています。このようにxの値が0に収束するような制御入力の与え方をいろいろと試していきます。
ON-OFF制御
xの値を0に収束させたい。そんなとき、どうすれば良いか。一番に思い付くのは、xが大きければ負の方向に力を加え、xが小さければ正の方向に力を加えることでしょう。
import matplotlib.pyplot as plt
x_list = []
t_list = []
dt = 0.1
m = 1.0 #質量[kg]
x = 1 #初期位置[m]
v = 0 #初速度[m/s]
f = 1 #入力[N]
def F(e): #制御入力
if x>0.8:
u = -f
elif x<-0.8:
u = f
else:
u = 0
return u
for i in range(int(50/dt)):
t = i*dt
x += dt*v
v += dt*F(x)/m
x_list.append(x)
t_list.append(t)
plt.plot(t_list,x_list,color ='b')
plt.title('ON-OFF')
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()
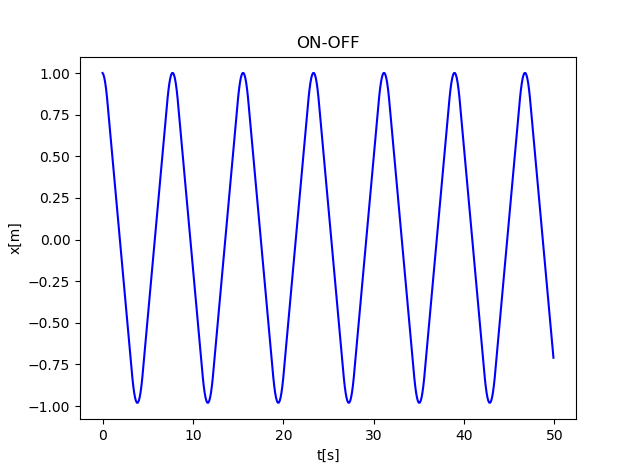
だめだ、収束しない
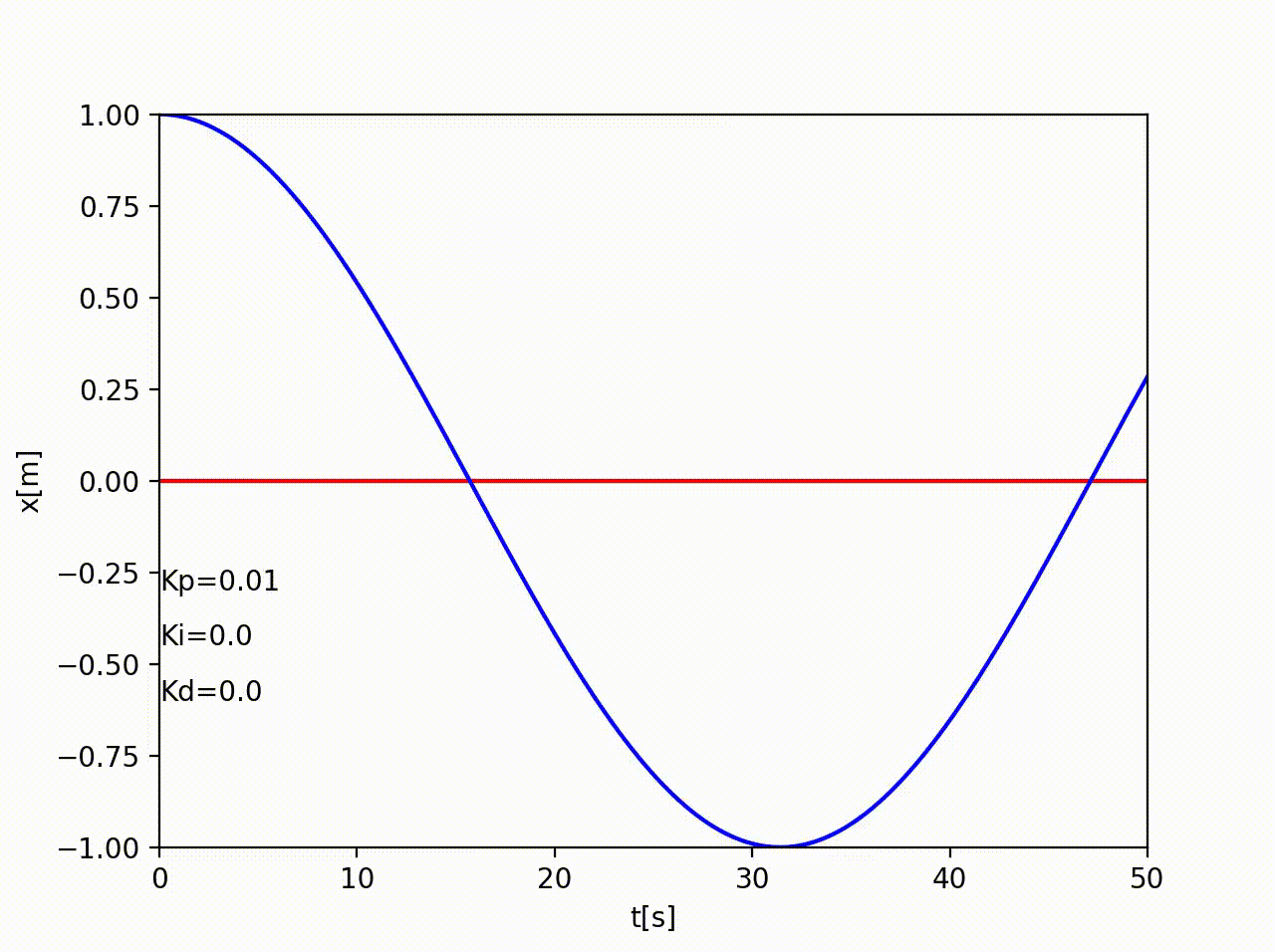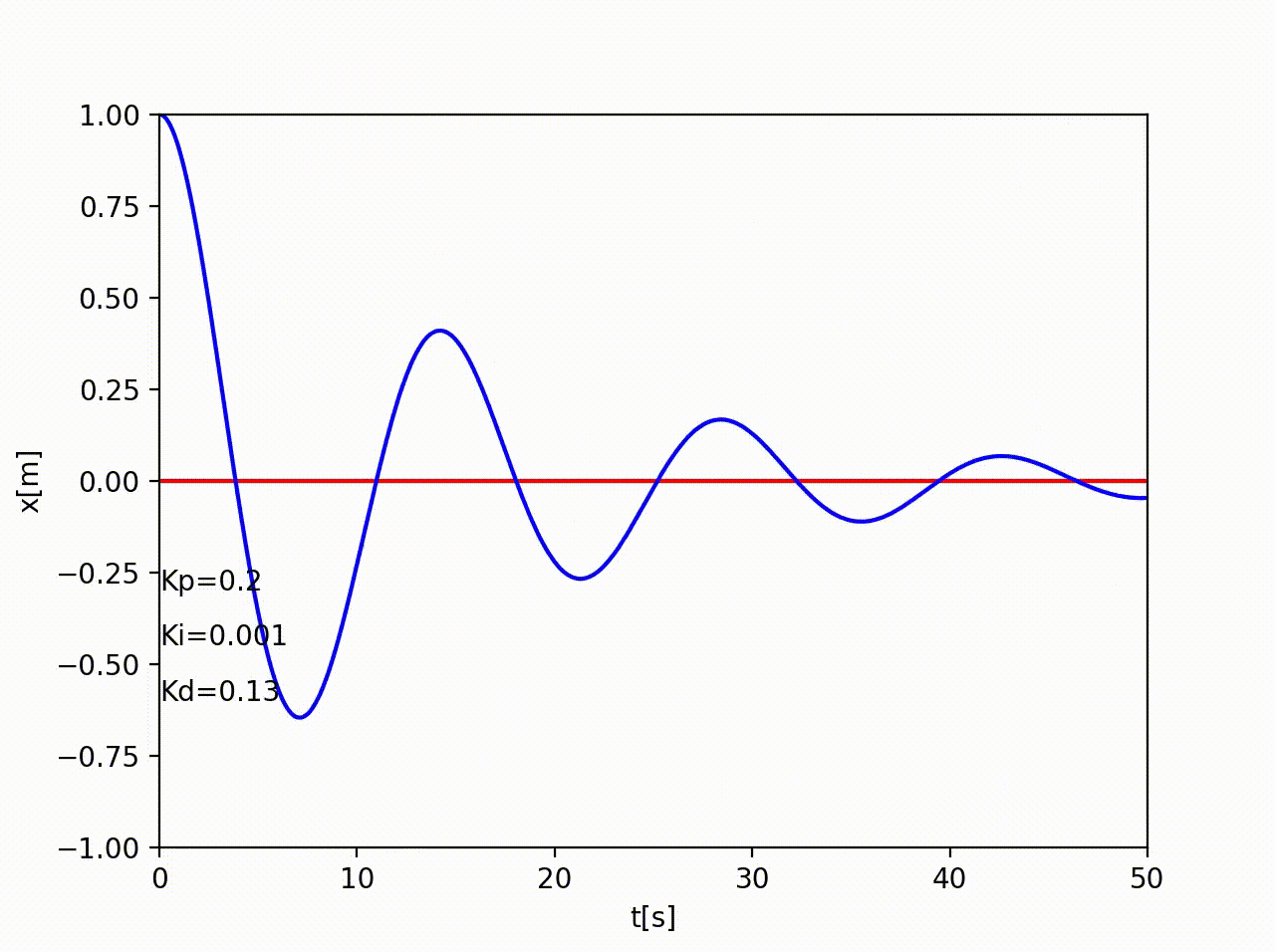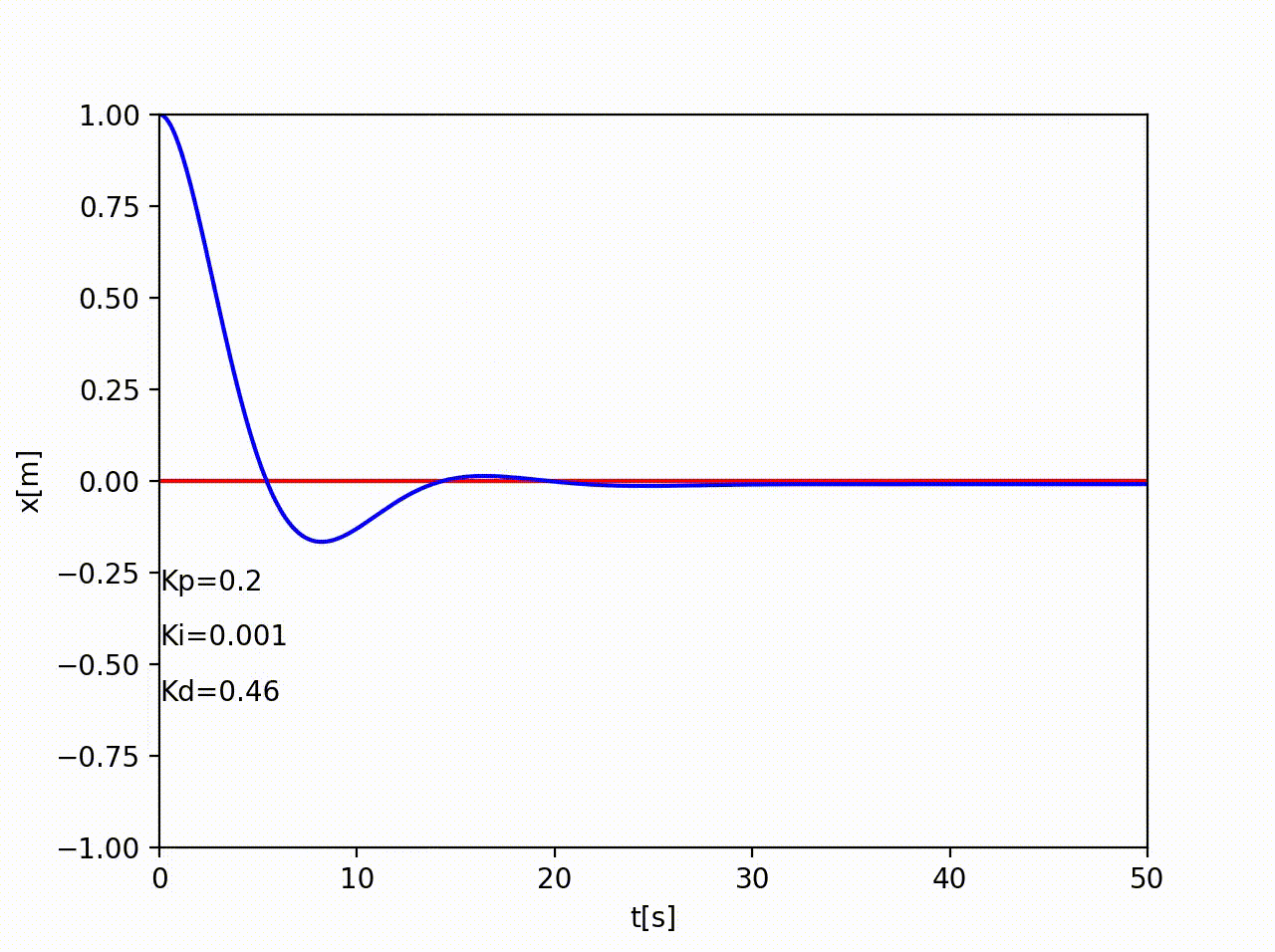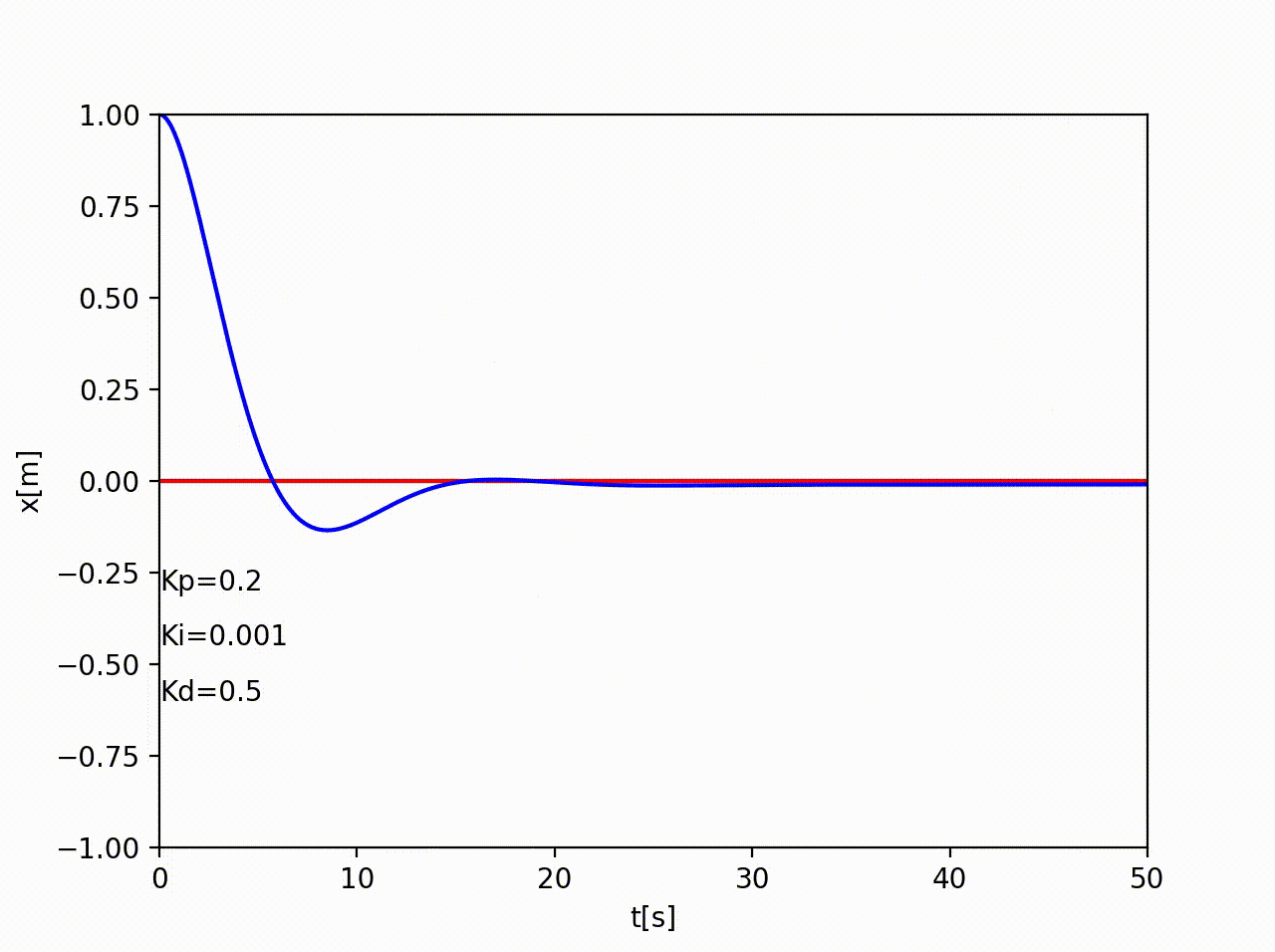
P制御( Proportional Controller )
目標値と現在値の差に応じて、力の入力を変えればうまくいくのではないか。つまり、目標値との差に比例した制御入力を与える。
import matplotlib.pyplot as plt
x_list = []
t_list = []
dt = 0.1
m = 1.0 #質量[kg]
x = 1 #初期位置[m]
v = 0 #初速度[m/s]
Kp = 0.3 #比例ゲイン
for i in range(int(50/dt)):
t = i*dt
x += dt*v
F = -x*Kp
v += dt*F/m
x_list.append(x)
t_list.append(t)
plt.plot(t_list,x_list,color ='b')
plt.title('Proportional-Controller')
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()
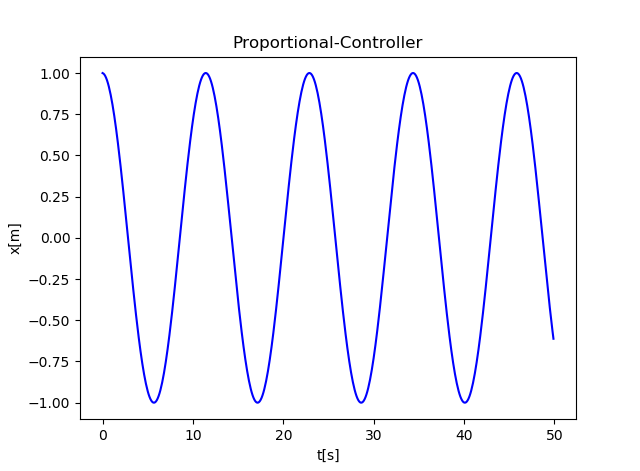
これは単振動。"位置に比例した力"はバネと同じなので、収束しない。(抵抗とかあったら収束する)
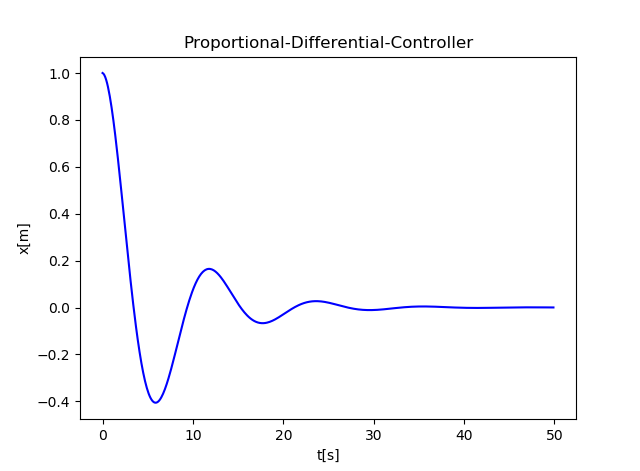
PD制御( Proportional-Differential Controller )
速度(位置の微分値)に比例した制御入力を追加する。変化を抑制する。
import matplotlib.pyplot as plt
x_list = []
t_list = []
dt = 0.1
m = 1.0 #質量[kg]
x = 1 #初期位置[m]
v = 0 #初速度[m/s]
Kp = 0.3 #比例ゲイン
Kd = 0.3 #微分ゲイン
for i in range(int(50/dt)):
t = i*dt
x += dt*v
F = -x*Kp -v*Kd
v += dt*F/m
x_list.append(x)
t_list.append(t)
plt.plot(t_list,x_list,color ='b')
plt.title('Proportional-Differential-Controller')
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()

収束した。
ここではノイズを考慮しないが、ノイズがある場合は微分値にローパスフィルタをかける必要がある。 (ノイズでギザギザの値は微分できないから)ローパスフィルタをかけた微分を不完全微分という。ローパスフィルタについては以下の記事で紹介しています。
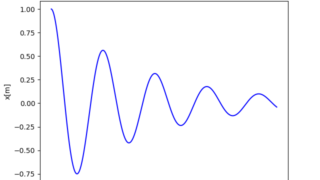
PID制御(Proportional-Integral-Differential Controller)
PD制御だと、目標値付近ではほとんど入力が無くなる→無限時間経たないと完全には0に収束しない。そこで、積分成分を追加する。いつまでも正の位置にあれば負の方向へ、負の位置に居れば正の方向へ制御入力が増えていく。
import matplotlib.pyplot as plt
x_list = []
t_list = []
dt = 0.1
m = 1.0 #質量[kg]
x = 1 #初期位置[m]
v = 0 #初速度[m/s]
w = 0
Kp = 0.2 #比例ゲイン
Kd = 0.5 #微分ゲイン
Ki = 0.01 #積分ゲイン
for i in range(int(50/dt)):
t = i*dt
x += dt*v
w += dt*x
F = -x*Kp -v*Kd -w*Ki
v += dt*F/m
x_list.append(x)
t_list.append(t)
plt.plot(t_list,x_list,color ='b')
plt.title('Proportional-Differential-Controller')
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()
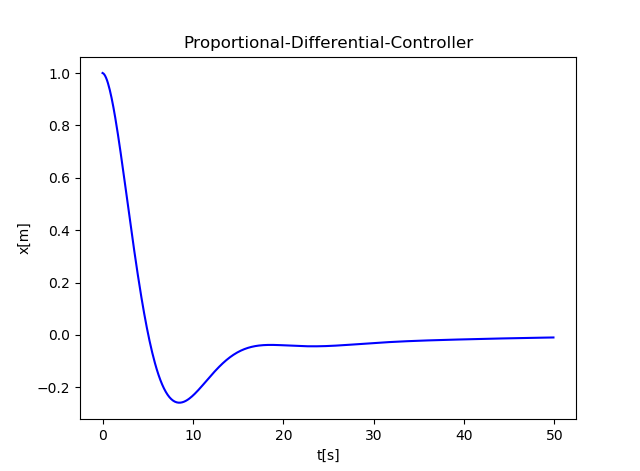
あとは、ゲインKp,Ki,Kdをうまく調節すればきれいに収束するようになる。
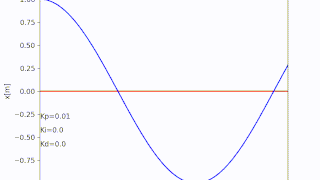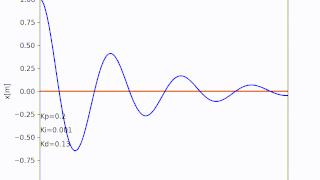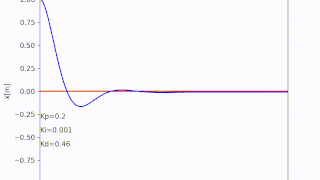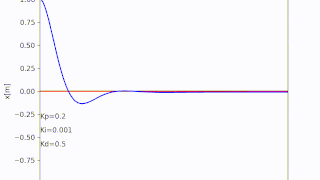
アニメーションにするとこんな感じ
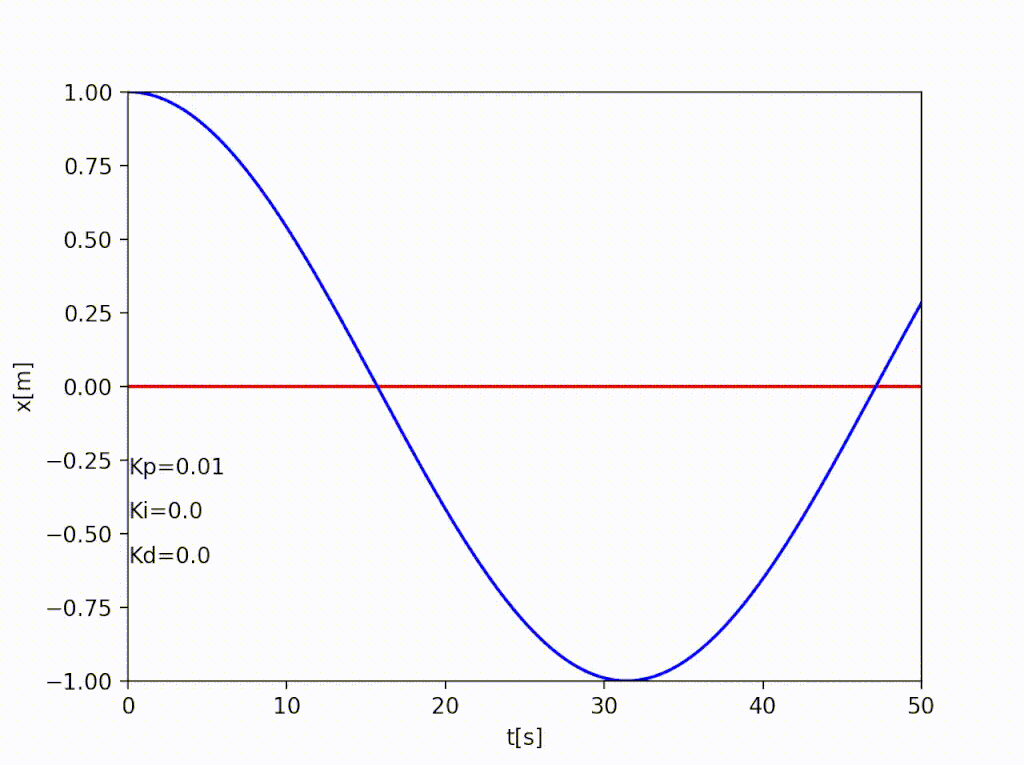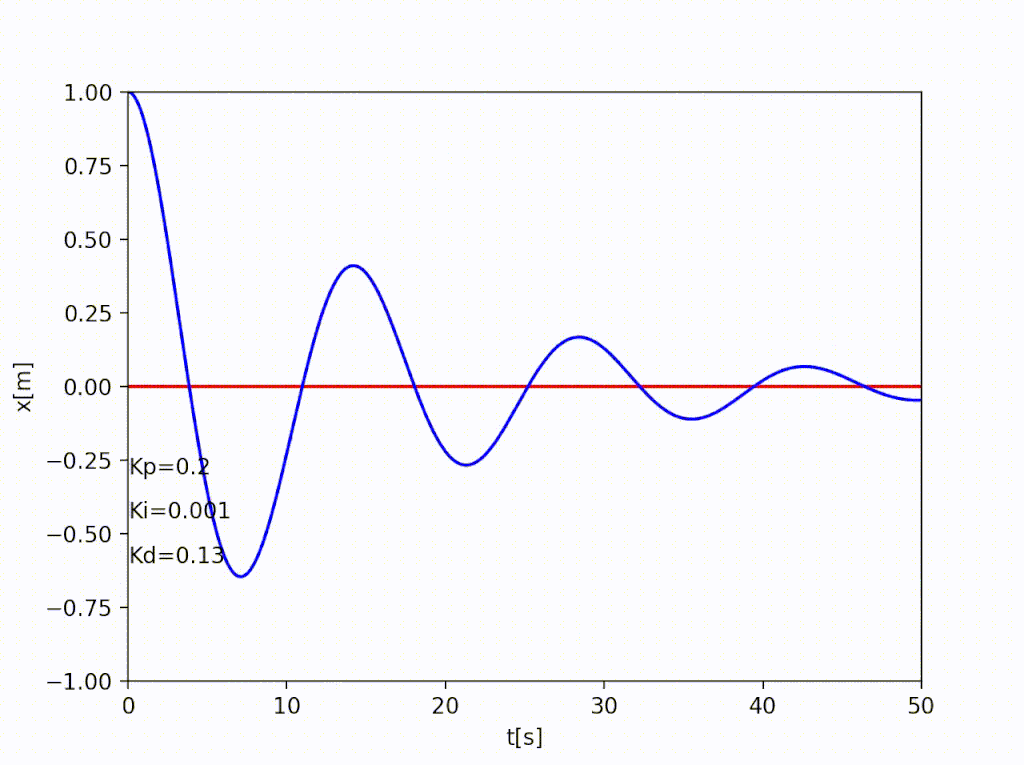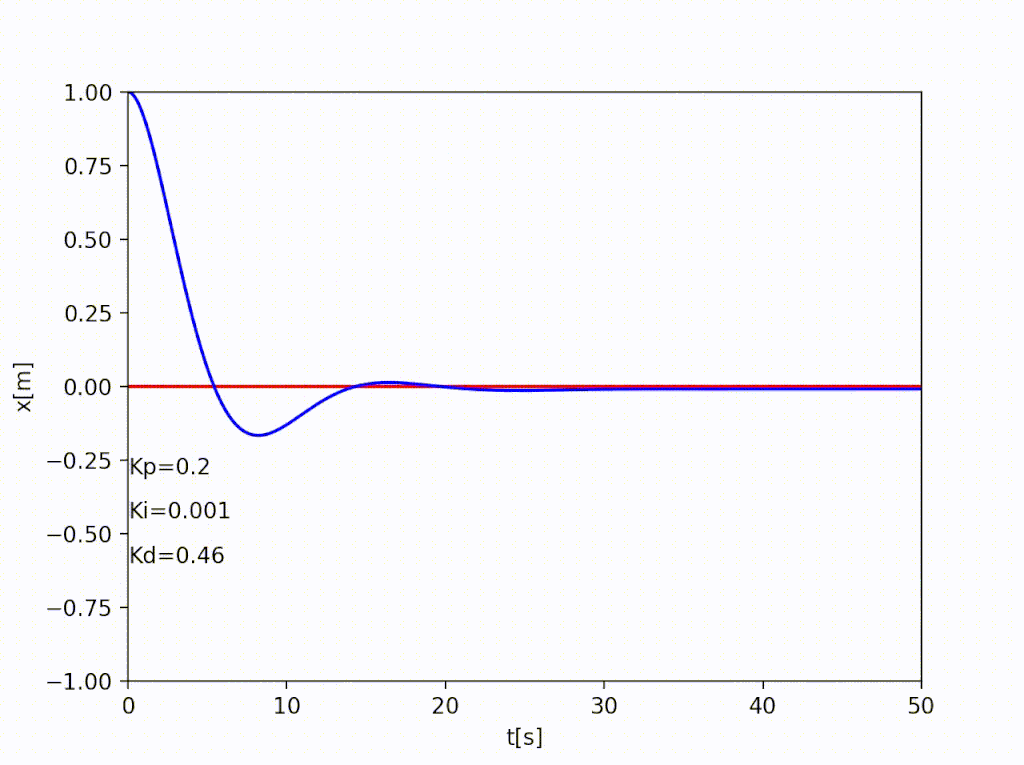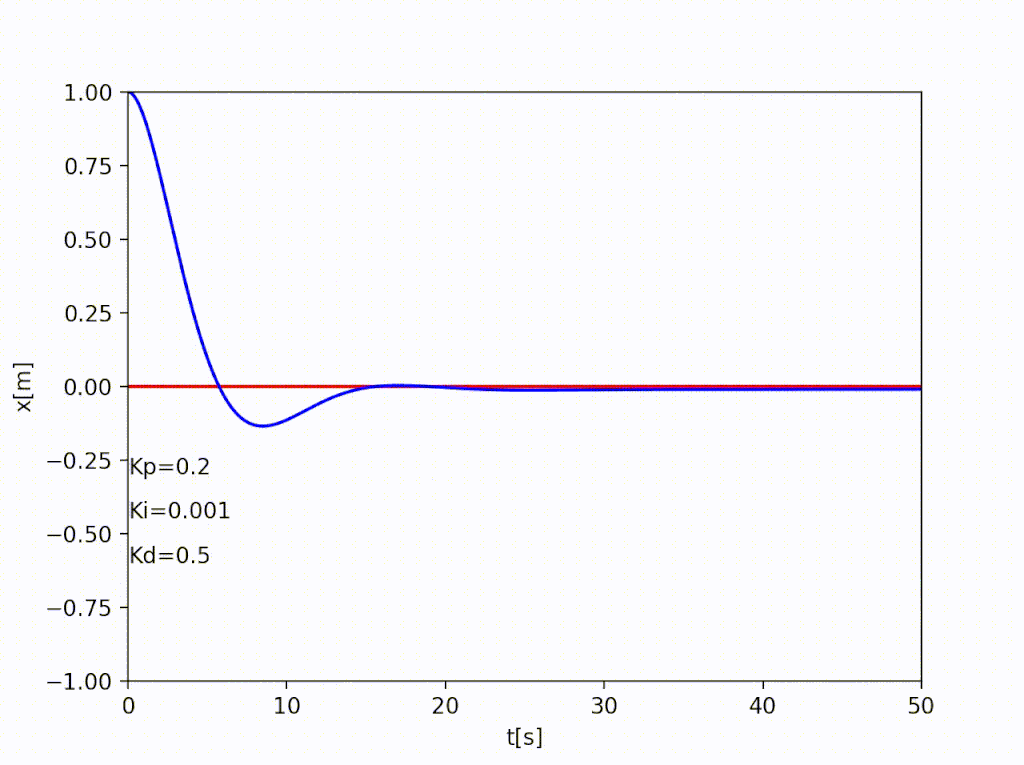
アニメーションはArtistAnimationを使って作成
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
fig, ax = plt.subplots()
ims = []
dt = 0.01
m = 1.0 #質量[kg]
Kp = 0.0
Kd = 0.0
Ki = 0.0
for j in range(100):
x_list = []
t_list = []
if Kp < 0.2: #比例ゲイン
Kp += 0.01
elif Ki < 0.001: #積分ゲイン
Ki += 0.001
elif Kd < 0.5: #微分ゲイン
Kd += 0.01
x = 1 #初期位置[m]
v = 0 #初速度[m/s]
w = 0
for i in range(int(50/dt)):
t = i*dt
x += dt*v
w += dt*x
F = -x*Kp -v*Kd -w*Ki
v += dt*F/m
x_list.append(x)
t_list.append(t)
tx1 = "Kp=" + str(round(Kp,3))
tx2 = "Ki=" + str(round(Ki,3))
tx3 = "Kd=" + str(round(Kd,3))
title1 = ax.text(0,-0.3,tx1)
title2 = ax.text(0,-0.45,tx2)
title3 = ax.text(0,-0.6,tx3)
im = plt.plot([0,50],[0,0],color='r')
im += plt.plot(t_list,x_list,color ='b')
ims.append(im + [title1] + [title2] + [title3])
ani = animation.ArtistAnimation(fig,ims,interval=100)
plt.ylim(-1,1)
plt.xlim(0,50)
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()
リンク












コメント