pythonでバネマスダンパ系のシミュレーションを行い、グラフを描画します。今回はオイラー法を用います。
リンク
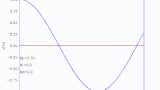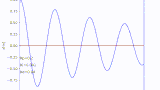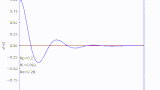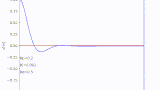
バネマス系
まずバネの運動方程式を立てます。加速度は \(a=\ddot{x}\) なので \(m\ddot{x} = f,f=-kx \) より、
$$m\ddot{x} +kx=0$$
これを\(v=\dot{x}\)を用いて1階の微分方程式で表すと
\[ \begin{eqnarray} \left\{ \begin{array}{l} \dot{x}=v \\ \dot{v}=-\frac{k}{m}x \end{array} \right. \end{eqnarray} \]
となる。時間がdtだけ進めばxの値はdt\(\times\dot{x}\), vの値はdt\(\times\dot{v}\) だけ増加する。つまり、tをdtずつ増加させたとき、xを dt\(\times v\) 、vを dt\(\times(-\frac{k}{m})x\) ずつ増加させれば良い。
import matplotlib.pyplot as plt
x_list = []
t_list = []
dt = 0.1
m = 1.0 #質量[kg]
k = 0.3 #ばね定数[N/m]
x = 1 #初期位置[m]
v = 0 #初速度[m/s]
for i in range(int(50/dt)):
t = i*dt #tをdtずつ増加
x += dt*(v) #xをdxずつ増加
v += dt*(-k/m*x) #vをdvずつ増加
x_list.append(x)
t_list.append(t)
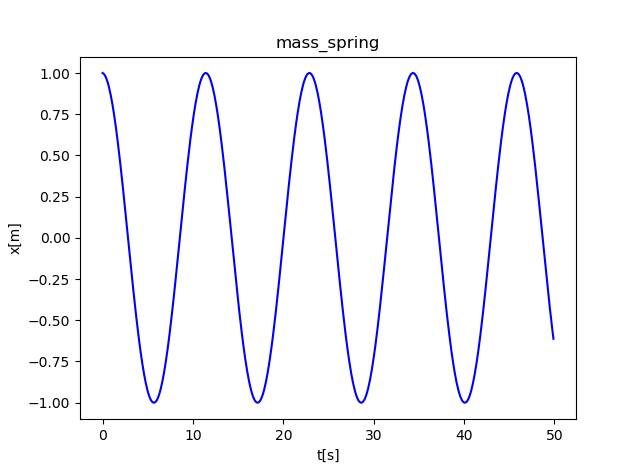
plt.plot(t_list,x_list,color ='b')
plt.title('mass_spring')
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()
バネマスダンパ系
運動方程式は
$$m\ddot{x} + c\dot{x} + kx=0$$
これを\(v=\dot{x}\)を用いて1階の微分方程式で表すと
\[ \begin{eqnarray} \left\{ \begin{array}{l} \dot{x}=v \\ \dot{v}=-\frac{1}{m}(kx + cv) \end{array} \right. \end{eqnarray} \]
import matplotlib.pyplot as plt
x_list = []
t_list = []
dt = 0.1
m = 1.0 #質量[kg]
k = 0.3 #ばね定数[N/m]
c = 0.1 #ダンパの減衰係数[N・s/s]
x = 1 #初期位置
v = 0 #初速度
for i in range(int(50/dt)):
t = i*dt #tをdtずつ増加
x += dt*(v) #xをdxずつ増加
v += dt/m*(-k*x -c*v) #vをdvずつ増加
x_list.append(x)
t_list.append(t)
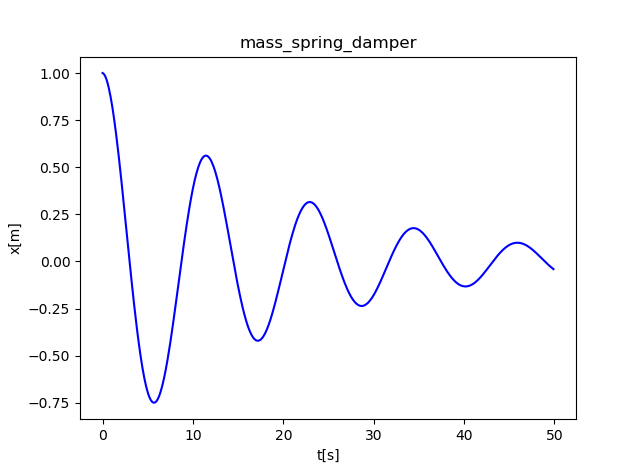
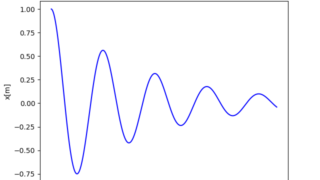
plt.plot(t_list,x_list,color ='b')
plt.title('mass_spring_damper')
plt.xlabel('t[s]')
plt.ylabel('x[m]')
plt.show()
リンク












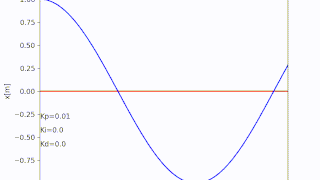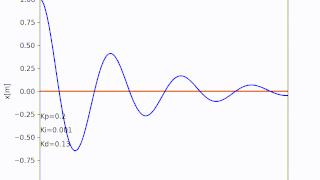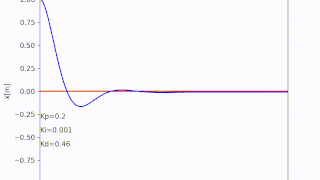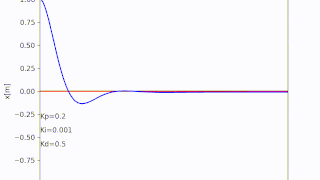
コメント